Thursday, 4 December 2014

PUMPS

A pump is a device that moves fluids (liquids or gases), or sometimes slurries, by mechanical action. Pumps can be classified into three major groups according to the method they use to move the fluid: direct lift, displacement, and gravity pumps.[1]
Pumps operate by some mechanism (typically reciprocating or rotary), and consume energy to perform mechanical work by moving the fluid. Pumps operate via many energy sources, including manual operation, electricity, engines, or wind power, come in many sizes, from microscopic for use in medical applications to large industrial pumps.
Mechanical pumps serve in a wide range of applications such as pumping water from wells, aquarium filtering, pond filtering and aeration, in the car industry for water-coolingand fuel injection, in the energy industry for pumping oil and natural gas or for operating cooling towers. In the medical industry, pumps are used for biochemical processes in developing and manufacturing medicine, and as artificial replacements for body parts, in particular the artificial heart and penile prosthesis.
In biology, many different types of chemical and bio-mechanical pumps have evolved, and biomimicry is sometimes used in developing new types of mechanical pumps.

Reciprocating pumps move the fluid using one or more oscillating pistons, plungers, or membranes (diaphragms), while valves restrict fluid motion to the desired direction.
Pumps in this category range from simplex, with one cylinder, to in some cases quad (four) cylinders, or more. Many reciprocating-type pumps are duplex (two) or triplex (three) cylinder. They can be either single-acting with suction during one direction of piston motion and discharge on the other, or double-acting with suction and discharge in both directions. The pumps can be powered manually, by air or steam, or by a belt driven by an engine. This type of pump was used extensively in the 19th century—in the early days of steam propulsion—as boiler feed water pumps. Now reciprocating pumps typically pump highly viscous fluids like concrete and heavy oils, and serve in special applications that demand low flow rates against high resistance. Reciprocating hand pumps were widely used to pump water from wells. Common bicycle pumps and foot pumps for inflation use reciprocating action.
These positive displacement pumps have an expanding cavity on the suction side and a decreasing cavity on the discharge side. Liquid flows into the pumps as the cavity on the suction side expands and the liquid flows out of the discharge as the cavity collapses. The volume is constant given each cycle of operation.

Rotodynamic pumps (or dynamic pumps) are a type of velocity pump in which kinetic energy is added to the fluid by increasing the flow velocity. This increase in energy is converted to a gain in potential energy (pressure) when the velocity is reduced prior to or as the flow exits the pump into the discharge pipe. This conversion of kinetic energy to pressure is explained by the First law of thermodynamics, or more specifically by Bernoulli's principle.
Dynamic pumps can be further subdivided according to the means in which the velocity gain is achieved.[5]
These types of pumps have a number of characteristics:
  1. Continuous energy
  2. Conversion of added energy to increase in kinetic energy (increase in velocity)
  3. Conversion of increased velocity (kinetic energy) to an increase in pressure head
A practical difference between dynamic and positive displacement pumps is how they operate under closed valve conditions. Positive displacement pumps physically displace fluid, so closing a valve downstream of a positive displacement pump produces a continual pressure build up that can cause mechanical failure of pipeline or pump. Dynamic pumps differ in that they can be safely operated under closed valve conditions (for short periods of time).
Posted by at No comments:

Wednesday, 3 December 2014

MINING IN INDIA- CASE STUDY B-TECH EVS

The Mining industry in India is a major economic activity which contributes significantly to the economy of India. The GDP contribution of the mining industry varies from 2.2% to 2.5% only but going by the GDP of the total industrial sector it contributes around 10% to 11%. Even mining done on small scale contributes 6% to the entire cost of mineral production. Indian mining industry provides job opportunities to around 700,000 individuals.
India is the largest producer of sheet mica, the third largest producer of iron ore and the fifth largest producer of bauxite in the world. India's metal and mining industry was estimated to be $106.4bn (£68.5bn) in 2010.
However, the mining in India is also infamous for human right violations and environmental pollution. The industry has been hit by several high profile mining scandals in recent times.

The tradition of mining in the region is ancient and underwent modernization alongside the rest of the world as India gained independence in 1947. The economic reforms of 1991 and the 1993 National Mining Policy further helped the growth of the mining sector.[3] India's minerals range from both metallic and non-metallic types. The metallic minerals comprise ferrous and non-ferrous minerals, while the nonmetallic minerals comprise mineral fuels, precious stones, among others.[4]
D.R. Khullar holds that mining in India depends on over 3,100 mines, out of which over 550 are fuel mines, over 560 are mines for metals, and over 1970 are mines for extraction of nonmetals.The figure given by S.N. Padhi is: 'about 600 coal mines, 35 oil projects and 6,000 metalliferous mines of different sizes employing over one million persons on a daily average basis.Both open cast mining and underground miningoperations are carried out and drilling/pumping is undertaken for extracting liquid or gaseous fuels. The country produces and works with roughly 100 minerals, which are an important source for earning foreign exchange as well as satisfying domestic needs.[3] India also exports iron ore, titanium, manganese, bauxite, granite, and imports cobalt, mercury, graphite etc.[3]
Unless controlled by other departments of the Government of India mineral resources of the country are surveyed by the Indian Ministry of Mines, which also regulates the manner in which these resources are used.The ministry oversees the various aspects of industrial mining in the country. Both the Geological Survey of India and the Indian Bureau of Mines are also controlled by the ministry.Natural gas,petroleum and atomic minerals are exempt from the various activities of the Indian Ministry of Mines.
Posted by at No comments:

Tuesday, 2 December 2014

WATCH FOR YOU


Posted by at 1 comment:

Monday, 1 December 2014

HIV/AIDS

Human immunodeficiency virus infection and acquired immune deficiency syndrome (HIV/AIDS) is a disease spectrum of the human immune system caused by infection with human immunodeficiency virus (HIV).[1][2][3] Following initial infection, a person may experience a brief period of influenza-like illness. This is typically followed by a prolonged period without symptoms. As the infection progresses, it interferes more and more with the immune system, making the person much more susceptible to common infections like tuberculosis, as well as opportunistic infections and tumors that do not usually affect people who have working immune systems. The late symptoms of the infection are referred to as AIDS. This stage is often complicated by an infection of the lung known as pneumocystis pneumonia, severe weight loss, a type of cancer known as Kaposi's sarcoma, or other AIDS-defining conditions.
HIV is transmitted primarily via unprotected sexual intercourse (including anal and oral sex), contaminated blood transfusions, hypodermic needles, and from mother to child during pregnancy, delivery, or breastfeeding.[4] Some bodily fluids, such as saliva and tears, do not transmit HIV.[5] Prevention of HIV infection, primarily through safe sex and needle-exchange programs, is a key strategy to control the spread of the disease. There is no cure or vaccine; however, antiretroviral treatment can slow the course of the disease and may lead to a near-normal life expectancy. While antiretroviral treatment reduces the risk of death and complications from the disease, these medications are expensive and have side effects. Without treatment, the average survival time after infection with HIV is estimated to be 9 to 11 years, depending on the HIV subtype.[6]
Genetic research indicates that HIV originated in west-central Africa during the late nineteenth or early twentieth century.[7] AIDS was first recognized by the United StatesCenters for Disease Control and Prevention (CDC) in 1981 and its cause—HIV infection—was identified in the early part of the decade.[8] Since its discovery, AIDS has caused an estimated 36 million deaths worldwide (as of 2012).[9] As of 2012, approximately 35.3 million people are living with HIV globally.[9] HIV/AIDS is considered apandemic—a disease outbreak which is present over a large area and is actively spreading.[10]
HIV/AIDS has had a great impact on society, both as an illness and as a source of discrimination. The disease also has significant economic impacts. There are manymisconceptions about HIV/AIDS such as the belief that it can be transmitted by casual non-sexual contact. The disease has also become subject to many controversies involving religion. It has attracted international medical and political attention as well as large-scale funding since it was identified in the 1980s


HIV/AIDS
Classification and external resources
A red ribbon in the shape of a bow
The red ribbon is a symbol for solidarity with HIV-positive people and those living with AIDS.



Posted by at No comments:

Sunday, 30 November 2014

DC MACHINES


Posted by at No comments:

BOOKS


Posted by at No comments:

Saturday, 29 November 2014

Telegrapher's equations

The telegrapher's equations (or just telegraph equations) are a pair of linear differential equations which describe the voltage and current on an electrical transmission line with distance and time. They were developed by Oliver Heaviside who created the transmission line model, and are based on Maxwell's Equations.
Schematic representation of the elementary component of a transmission line.
The transmission line model represents the transmission line as an infinite series of two-port elementary components, each representing an infinitesimally short segment of the transmission line:
  • The distributed resistance R of the conductors is represented by a series resistor (expressed in ohms per unit length).
  • The distributed inductance L (due to the magnetic field around the wires, self-inductance, etc.) is represented by a series inductor (henries per unit length).
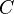  • The capacitance C between the two conductors is represented by a shunt capacitor C (farads per unit length).
  • The conductance G of the dielectric material separating the two conductors is represented by a shunt resistor between the signal wire and the return wire (siemensper unit length).
The model consists of an infinite series of the elements shown in the figure, and that the values of the components are specified per unit length so the picture of the component can be misleading. R, L, C, and G may also be functions of frequency. An alternative notation is to use R', L', C' and G' to emphasize that the values are derivatives with respect to length. These quantities can also be known as the primary line constants to distinguish from the secondary line constants derived from them, these being the propagation constant,attenuation constant and phase constant.
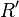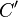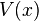The line voltage V(x) and the current I(x) can be expressed in the frequency domain as
\frac{\partial V(x)}{\partial x} = -(R + j \omega L)I(x)
\frac{\partial I(x)}{\partial x} = -(G + j \omega C)V(x).
When the elements R and G are negligibly small the transmission line is considered as a lossless structure. In this hypothetical case, the model depends only on the L and C elements which greatly simplifies the analysis. For a lossless transmission line, the second order steady-state Telegrapher's equations are:
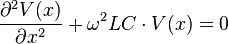
\frac{\partial^2V(x)}{\partial x^2}+ \omega^2 LC\cdot V(x)=0
\frac{\partial^2I(x)}{\partial x^2} + \omega^2 LC\cdot I(x)=0.
These are wave equations which have plane waves with equal propagation speed in the forward and reverse directions as solutions. The physical significance of this is that electromagnetic waves propagate down transmission lines and in general, there is a reflected component that interferes with the original signal. These equations are fundamental to transmission line theory.
If R and G are not neglected, the Telegrapher's equations become:
\frac{\partial^2V(x)}{\partial x^2} = \gamma^2 V(x)
\frac{\partial^2I(x)}{\partial x^2} = \gamma^2 I(x)
where γ is the propagation constant
\gamma = \sqrt{(R + j \omega L)(G + j \omega C)}
and the characteristic impedance can be expressed as
Z_0 = \sqrt{\frac{R + j \omega L}{G + j \omega C}}.
The solutions for V(x) and I(x) are:
V(x) = V^+ e^{-\gamma x} + V^- e^{\gamma x} \,
I(x) = \frac{1}{Z_0}(V^+ e^{-\gamma x} - V^- e^{\gamma x}). \,
The constants V^\pm and I^\pm must be determined from boundary conditions. 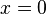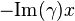For a voltage pulse V_{\mathrm{in}}(t) \,, starting at x=0 and moving in the positive x-direction, then the transmitted pulse V_{\mathrm{out}}(x,t) \, at position xcan be obtained by computing the Fourier Transform, \tilde{V}(\omega), of V_{\mathrm{in}}(t) \,, attenuating each frequency component by e^{\mathrm{-Re}(\gamma) x} \,, advancing its phase by \mathrm{-Im}(\gamma)x \,, and taking the inverse Fourier Transform. The real and imaginary parts of \gamma can be computed as
\mathrm{Re}(\gamma) = (a^2 + b^2)^{1/4} \cos(\mathrm{atan2}(b,a)/2) \,
\mathrm{Im}(\gamma) = (a^2 + b^2)^{1/4} \sin(\mathrm{atan2}(b,a)/2) \,
where atan2 is the two-parameter arctangent, and
a \equiv \omega^2 LC \left[ \left( \frac{R}{\omega L} \right) \left( \frac{G}{\omega C} \right) - 1 \right]
b \equiv \omega^2 LC \left( \frac{R}{\omega L} + \frac{G}{\omega C} \right).
For small losses and high frequencies, to first order in R / \omega L and G / \omega C one obtains
\mathrm{Re}(\gamma) \approx \frac{\sqrt{LC}}{2} \left( \frac{R}{L} + \frac{G}{C} \right) \,
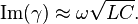
\mathrm{Im}(\gamma) \approx \omega \sqrt{LC}. \,
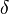Noting that an advance in phase by - \omega \delta is equivalent to a time delay by \delta, V_{out}(t) can be simply computed as
V_{\mathrm{out}}(x,t) \approx V_{\mathrm{in}}(t - \sqrt{LC}x) e^{- \frac{\sqrt{LC}}{2} \left( \frac{R}{L} + \frac{G}{C} \right) x }. \,
Posted by at No comments:
Subscribe to: Posts (Atom)